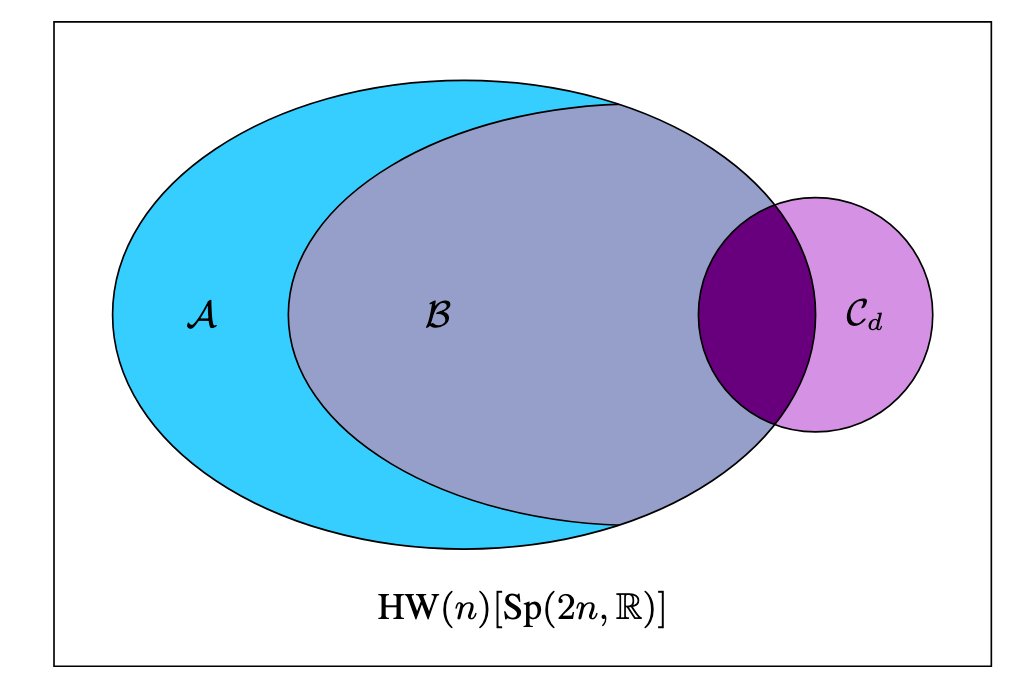
New paper out (my first 1st author!). We prove that two large sets (A,B in figure) of continuous-variable quantum circuits with input 0-GKP states are efficiently simulatable (solvable with regular computers). See the popular summary below.
Quantum computers – devices in which quantum information can be encoded, processed, and read out – are expected to solve certain computational tasks exponentially faster than classical computers. This property is referred to as quantum advantage and has recently motivated a global effort toward building a quantum computer. But which quantum computing architectures are able to provide quantum advantage and which are not? Beyond the fundamental interest, being able to trace a boundary separating computationally useful quantum computing architectures, capable of providing computational speed-up, from classically efficiently simulatable ones is of technological importance in order to design devices capable of outperforming classical computation. Our work contributes to tracing this boundary.
We focus on quantum computer architectures whereby the information is encoded into continuous variables (CVs). This approach relies on quantized variables with a continuous spectrum, such as the position and momentum quadratures of the electromagnetic field. An example of such an encoding procedure is known as the Gottesman-Kitaev-Preskill (GKP) encoding, using GKP states. Architectures using this encoding allow for increased resilience to noise, with respect to architectures using discrete-variable systems.
Our work demonstrates that a large class of quantum circuits with input GKP states prepared to encode computational states such as 0 and 1 is efficiently simulatable with classical computers. We, therefore, demonstrate that these circuits are not capable of achieving quantum advantage. Our findings contribute therefore to drawing a divide between computationally useful and useless architectures of quantum computers.
https://quantum-journal.org/papers/q-2022-12-01-867/