Background
Zeno of Elea lived around 2500 years ago and established a set of philosophical problems still taught by philosophers. Despite no surviving writings by Zeno, we can learn about the concept known as Zeno’s arrow paradox from Aristotle’s writings. The paradox has inspired a particularly intriguing concept in quantum mechanics: the quantum zeno effect. By just observing a particular system you can stop it from moving. Using IBM’s quantum composer I’ll show you how to try this experiment yourself on a real quantum computer.
If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless.
Aristotle – Physics VI
Imagine recording an arrow soaring through the air with a high speed camera. When we play the clip we see that it follows a smooth trajectory towards its target. However, at each infintesimal point in time, or every frame, the arrow is stationary. This apparent paradox highlights the concept of discrete and continuous motion and is resolved by realising that the instantaneous velocity of a moving arrow can never be truly zero.
Quantum Zeno Effect
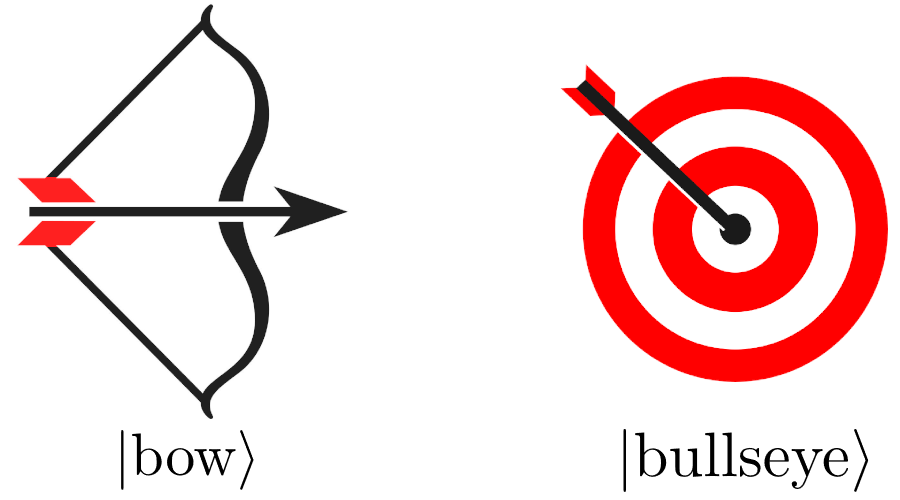
The quantum Zeno effect, on the other hand, demonstrates something highly suprising. Here we replace the arrow with a quantum arrow that can only be either in the bow or in the bullseye, or in a superposition of the two. By creating a force acting on the bow, to push the arrow towards the bullseye, we go from the state 
to 
.
Mathematically we can represent this as the state of the system evolving under a Hamiltonian of the form
![\[H=\frac{1}{T}(\ket{\text{bow}}\bra{\text{bullseye}} + \ket{\text{bullseye}}\bra{\text{bow}})\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-c01cf412e55789307d067a7678ea6b70_l3.png "Rendered by QuickLaTeX.com")
where we have defined a time period 
which dictates the speed of the evolution. This equation is solved using the Schrödinger equation. The state of the system at later times is
![\[\ket{\psi(t)}=\cos(\frac{2\pi t}{T})\ket{\text{bow}}+\sin(\frac{2\pi t}{T})\ket{\text{bullseye}}\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-6a9e297263a1177c77994abb900e6ee7_l3.png "Rendered by QuickLaTeX.com")
Something strange happens when we measure the state of a quantum system. It collapses into only one of the two states. When this happens the time evolution starts again, from this new state. If we keep measuring the system we can actually stop it from evolving in time!
Building the quantum circuit
The IBM Q allows us to explore this concept on a real quantum device. We will create a moving system which we will allow to evolve in time, like our arrow through the air.
We will then measure the state of our qubit repeatedly. By doing so the qubit will not be able to change state.
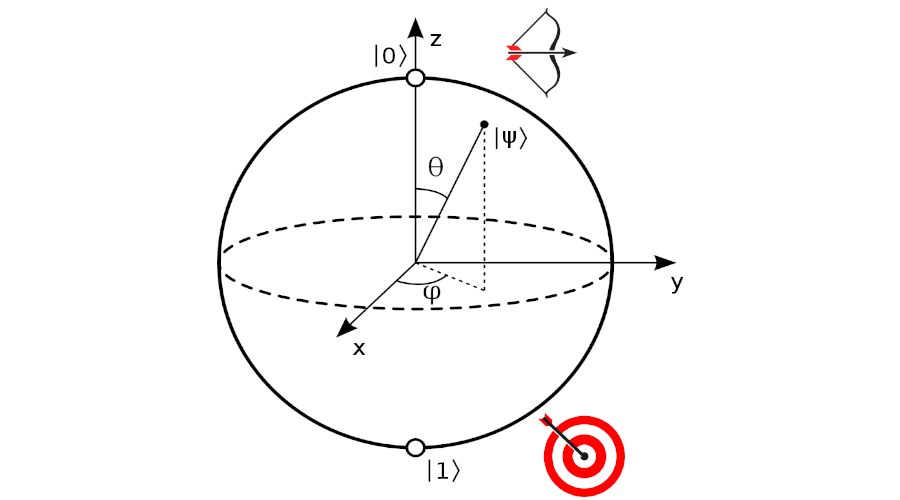
To start we need to decide where we will begin and where we want to end. To keep things simple lets just start our qubit in the state 0 and launch it towards the state 1. Coincidently, we can imagine our qubit as an arrow pointing to the surface of a sphere. If the arrow is pointing upwards, the qubit is in the state 0 and if it’s pointing down then it’s at 1.
The IBM Q automatically initialises our qubit in the 0 state. To test this we can try out a test circuit which simply measures our target (middle) qubit. The output tells us that all the qubits were measured to be in state 0.
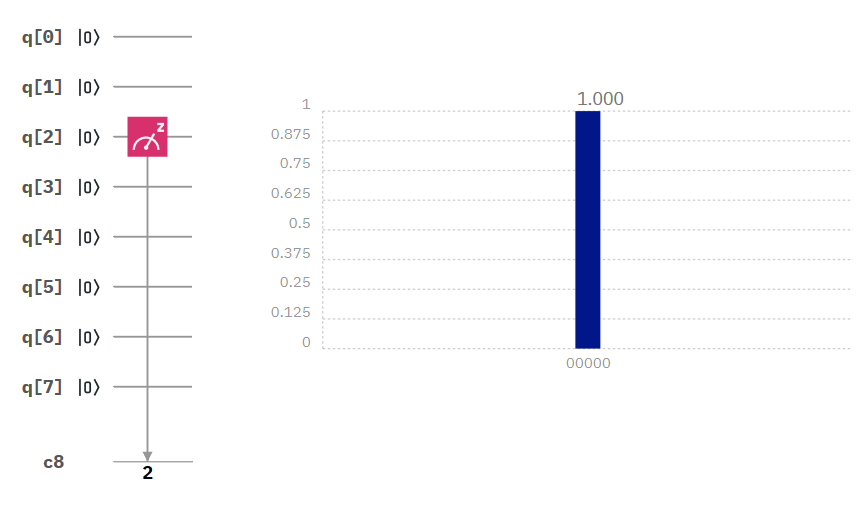
Hello World: the qubits start in the state 00000
How do we let our state evolve in time? Luckily the IBM Q is a universal quantum computer, meaning we could, in theory, run any classical algorithm we like. The operation we choose is a rotation. We can tell the quantum computer to rotate our state around the bloch sphere by some angle. We have five qubits so we pick to rotate the qubit a fifth of the way around the bloch sphere.
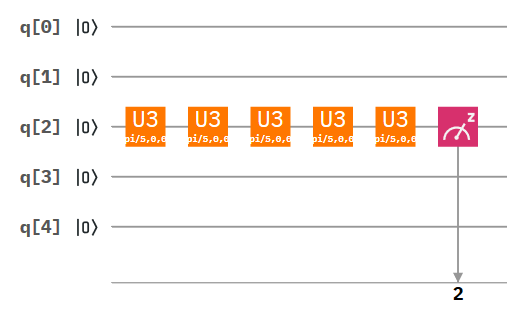
The qubit is rotated by 180 degrees and is measured to be 1
After doing this five times the result is not suprising, we end up with a 1 every time: the arrow has made it from the bow to the bullseye!
Adding Measurement
But what happens if we place a detector in the way of each of the rotations? This is equivelant to creating a CNOT gate which has the effect of switching the state of the 
of a target qubit. Using the principle of deffered and implicit measurment (which states that if we leave some quantum wires untouched we can assume they are measured), we create the effect of observing the state of our middle qubit after each rotation.
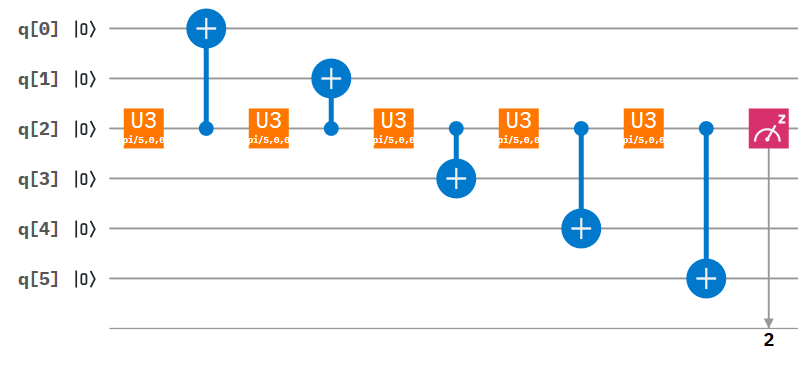
We add CNOT gates to measure the state of each qubit after each rotation.
Running the quantum algorithm
First lets try running the alogirthm on IBMs circuit simulator to check we get the result we expect. The number of times each result was given is presented in a histogram.
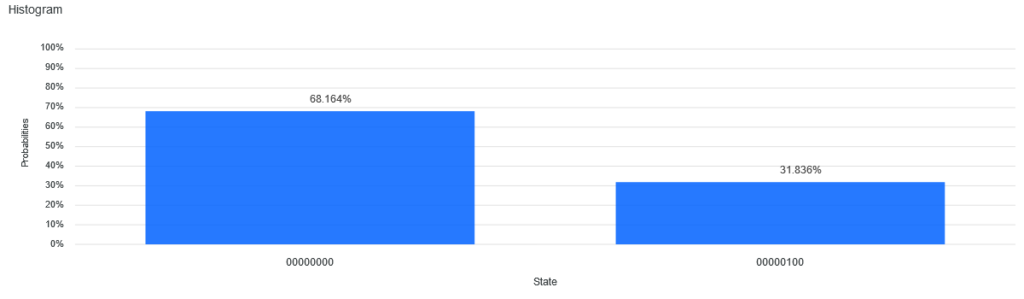
Results of the simulation
We see that our middle qubit remains in its 
state 68% of the time! To see why, consider the evolution after each gate rotation. The state of the qubit will be 
. Using our measurement gadget we see that the qubit will be projected either into the state with probability 
or into 
with probability 
. Repeating this process a further 
times we see that the chance of remaining in state is 
. By accounting for more complex transition including jumping into state and then jumping back to , we recover the expected probability.
Conclusion
We can now send this circuit to the real quantum computer and we see that we have succesfully stopped the time evolution of our qubit about 50% of the time!
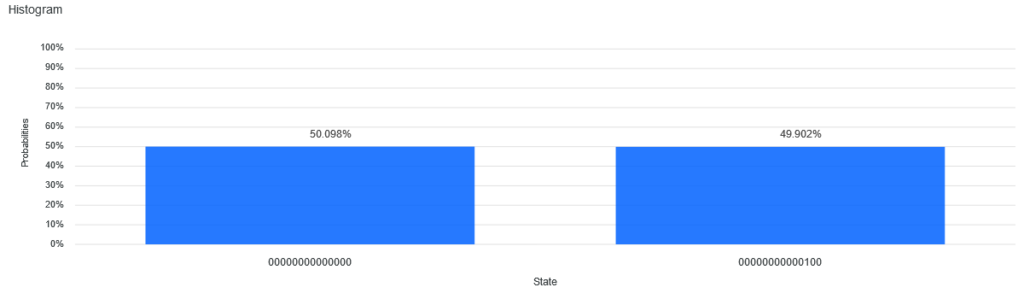
Results from IBM Q on device ibmq_16_melbourne
So the result appears not to be perfect – the result isn’t exaclty what is expected from the theory. This is due to two reasons. First, the IBM Q only has limited connectivity. This means the circuit needs to be broken down and remodelled before it can run on the quantum computer. This makes the circuit more complicated and it takes longer to run. The qubits are also vunerable to noise. Extremely subtle effects can have the effect of shifting the states of the qubits and destroying their coherence.
The result of the quantum zeno effect demonstrates the suprising and seemingly paradoxical world of quantum mechanics. The measurment problem is largely unresolved and is explored in great detail in Adam Becker’s most recent book ‘What is real?’. Exaclty why measurement has the effect of collapsing the wavefunction, or splitting the unvierse in two as the many world theorists argue, is unknown.
Not only does quantum computing have the power to unlock many of the key mysteries of chemisty, technology and health, but I hope it can also help us to answer deep fundamental questions about the nature of our universe.
