Introduction
Google has just announced a groundbreaking result. They have built a device which they claim demonstrates quantum supremacy.
I will explain what their result really means. I’ll go through the algorithm that they claim would take thousands of years to run on a classical computer, and yet their quantum computer only took a couple of minutes to calculate.
I’ll also take a look at IBM’s recent blog post and scientific paper which has received lots of media attention over the last couple of days. They claim that Google’s result is not as impressive as originally thought.
But first, let’s try to understand why there has been some push back to this term. And why I believe that the phrase should be avoided.
Supremacy
I am immersed within the world of quantum technology. When I hear the word supremacy, I think of one thing: quantum supremacy. Others have pointed out that to many people the phrase simply means “white supremacy”. At first, I thought the idea of not using a word in the English language because of its association to racists seemed a bit far fetched. The word has existed far longer than the connotations that come along with it. To help me understand the link, I searched Google’s nGram corpus. The query showed that only around 6% of the uses of the word in British English are preceded by the word “white”. However, change the search to American English and this number rises to more than 20%.
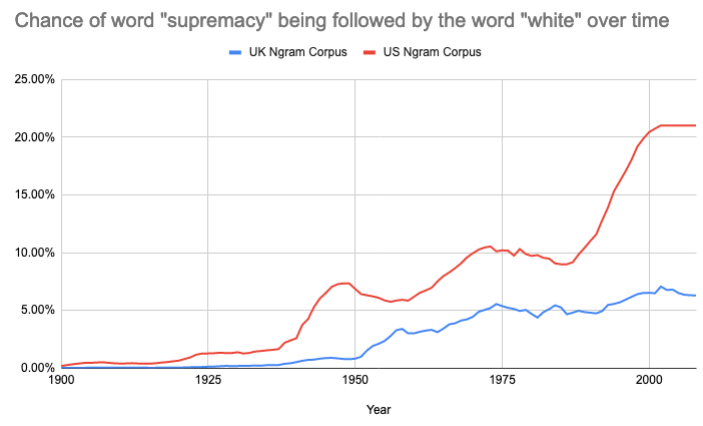
Perhaps this association is somewhat more visceral in American English. In any case, I must recognise my white privilege and acknowledge that my naivety should not be an excuse for using a word that people across the world associate with violence. White supremacy has a violent past and is still prevalent throughout our society. From violent hate attacks and terrorism to a sympathising US president, this is not something I want anyone to associate with my work. I believe that the scientific community should be as open and diverse as possible. By using a different term we can create a more welcoming community to all. Of course, our efforts should not stop here, but it is a simple and tiny change which signals the direction we should be moving in. The rest of this blog post will be free from the word!
Quantum Advantage
Many have suggested that we forget the term and use a different one: quantum advantage. At first glance, this seems like a good idea. However, quantum advantage has the specific meaning that a quantum computer is able to perform useful calculations faster than a classical computer.
By shifting to this phrase (e.g. Google achieves quantum advantage) we upgrade the Google result to something that it’s not. Google’s calculation was essentially useless! At least, useless except for proving that quantum computers can do at least one calculation faster than the best known classical algorithms.
I think simply shifting to this new phrase creates added confusion to an already incredibly complex topic. We want to avoid situations like presidential candidates declaring that no code is uncrackable!
Google achieving quantum computing is a huge deal. It means, among many other things, that no code is uncrackable. https://t.co/AghqDAYs66
— Andrew Yang? (@AndrewYang) September 21, 2019
If anything, I think shifting to this phrase will increase confusion!
Google has launched the era of quantum advantage
While I think that using a term which implies domination over classical computation is probably a bad idea, it is clear that we have just passed a huge milestone.
To understand why this is such a big deal, we need to understand a little bit of complexity theory. To keep it brief, we don’t know whether quantum computers can do things that classical computers can’t. This would make them entirely useless and there is no hard proof that this won’t one day happen. In fact, as we learn more about quantum computers, there are three possibilities:
1) Classical computers are actually able to solve all calculations in a time that increases polynomially with respect to the size of the input. There are some problems which we expect can only be solved in exponential time. The most famous example is factoring. Each digit we add to the number we wish to factorise, the time it takes to solve roughly doubles. It would be extremely surprising if someone found an algorithm which can factor large numbers polynomially, but there’s no proof that it couldn’t one day happen.
2) It will turn out that quantum computers are actually only able to do calculations as fast as classical computers, due to physical limits (e.g. factoring will take just as long on a quantum computer).
3) Quantum computers can do certain calculations exponentially faster than classical computers. These calculations could involve factoring large numbers, breaking certain types of encryption, and solving physics problems in a few seconds that classical computers would take millions of years to solve.
So far, nobody has been able to prove which one of these is true. In fact if you prove or disprove the first one then you’ve just won a million dollars!
Most people believe that the third option is most likely. However, there are a few notable people who think that the second option will be shown true.
Google’s result seems to hint that the second option might be false and that those who suggested that quantum computers will never outperform classical computers are wrong. This is incredibly important for the future of computer science. Although their result did not solve any useful calculation, it did prove that quantum computing can be used to calculate things that a classical computer would take a long time to solve.
So, how do we ensure that we recognise this important milestone while also avoiding using a phrase that is offensive and misleading?
I suggest that the Google result should be considered the beginning of the era of quantum advantage.
Quantum computers process an exponential amount of data
The reason why quantum computers are expected to be much faster than classical computers is down to the way that they process information. But what does this mean and why do we care?
The important point is that using just a handful of quantum bits, a quantum computer can hold an exponential amount of information in their state. It’s important to note that this doesn’t mean we could actually store huge amounts of information on a quantum computer like a hard drive. However, the quantum computer can perform calculations that depend on this information.
To understand what this means let’s pretend we have a quantum computer which has 100 perfect qubits. Using a simple procedure that I outline below, a quantum computer would be able to hold more bits of information than there are atoms in the earth. To understand how, and why this doesn’t mean that we can save all this information, we need to first understand classical information.
A classical computer stores data as 0s and 1s. If we have 
bits we can encode information (like a word, or an image) in 
different ways. Let’s restrict the size of our quantum computer to 10 quantum bits, to make things a bit easier. If we have 10 quantum bits, we can store many different combinations of these bits at the same time. We can even encode information within the probability of observing these combinations.
To see how to do this, let’s consider a 10 qubit quantum computer. We denote the state of our quantum computer using a wavefunction. This wavefunction tells us the probability of observing each possible combination. For our 10 qubit quantum computer, the wavefunction looks something like
![\[|\psi\rangle=a_1|0000000000\rangle+a_2|0000000001\rangle+a_3|0000000010\rangle+\dots +a_{1024}|1111111111\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-2e891668586383e4473d669fbd1bb793_l3.png "Rendered by QuickLaTeX.com")
where each letter 
is a complex number which roughly tells us the probability of observing the corresponding combination 
of our bits. These complex numbers are allowed to vary within something called the Hilbert space. This is just a way of conceptualising the virtual storage space that we can encode in the state.
As I mentioned above, the nice thing about this encoding is that we have the ability to store exponentially more information than on a classical computer of the same number of bits. For example, we could use the values of as our new bits. This way we could encode 1024 bits of information on just 10 qubits. If we scale up our system to about 100 qubits, we can technically hold more bits of information than there are atoms in the earth.
The Problem…
There is a major flaw in our apparent data storage device. Once we observe the quantum state, spread over a variety of different combinations of values, the state collapses into a single state. We aren’t able to extract the information, only observe one of these combinations. Something that sounded extremely exciting now sounds useless. Why does it matter if we can encode so much information if we can’t decode it again?
The reason why this is still so exciting, despite not being able to store information like a hard drive, is that we can load the data in and then manipulate it in incredibly complicated ways. There are lots of calculations that we can do, that take a simple input and give a simple output but take many years and a huge amount of data storage to calculate. (For example, the energy levels of relatively simple molecules, factorising numbers, finding the shortest route between a handful of cities, what is the answer to life, the universe and everything?) This is where quantum computers may be useful. We don’t necessarily care about all the data that it generates along the way, we just want to know the output.
Superposition
Superposition is one of two elements that makes quantum computers so powerful. To understand how superposition works, let’s consider the simplest possible quantum computer, consisting of a single qubit. While a classical bit can be in either a 0 or 1 state, a quantum computer can exist in a combination of the two. We can think about our qubit as being represented by a coin. If the coin is lying on a table with heads pointing up, then the coin is in the 0 state. If the coin is pointing down then it is in the 1 state. We can also imagine balancing the coin on its side, pointing left, right, forwards or backwards. This would correspond to the qubit lying in a superposition of 0 and 1. Imagine striking your hand down on the coin. It would land with heads up or heads down with equal probability. The direction of the coin in the horizontal plane doesn’t affect its probability but it can be utilised in other ways.
Mathematically the qubit’s state is represented by a complex number, which tells us the likelihood of observing it in a 0 or a 1, along with some additional information about its phase. We can represent this state using a diagram of an arrow inside of a sphere. This diagram is known as the Bloch sphere and allows us to imagine the qubit as a physical arrow pointing in some direction. You can think of this direction as the direction that the heads of the coin is pointing. If we measure an arrow pointing upwards, then we will measure a 0. If we measure one pointing downwards, then we measure a 1. If it is halfway between then we get a 0 or a 1 with equal probability.
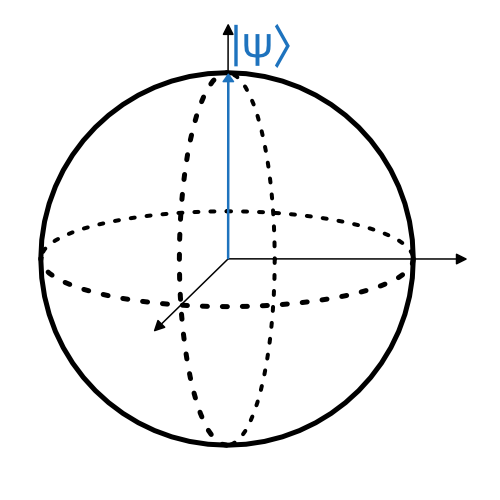
Bloch Sphere: Here we show the qubit in its 0 state. We can think of the arrow representing a form of probability. The direction indicates two things: the liklihood of the qubit being measured as a 0 (up) or a 1 (down) and also the phase which is represented as the rotation around the vertical axis.
We usually start our qubits in the 
state, corresponding to an arrow in the Bloch sphere pointing to the top pole. By rotating our qubit along its axes we can produce a state in a superposition. For example, consider a rotation of 90° around the 
axis. The state will be in an equal superposition of and 
. This means that when we measure it, the qubit will land in the classical state 0 or 1 with equal probability.
Calculations using Superposition
Taking our coin analogy further, let’s imagine we create a quantum computer with 8 qubits, all starting in the state. This is like preparing 8 coins lying heads up (the direction of the coin corresponds to the arrow on the Bloch sphere).
We then wait a little while and measure the result. The output is not surprising. We measure a classical result of 00000000.
A calculation consists of rotating our qubits around its axes. We allow rotations by 90° around 3 axes: the X axis, the Y axis, and an axis halfway between X and Y. These angles are chosen for two reasons: first, they are relatively easy to implement consistently, and second, using combinations of these three rotations we can rotate our coin/Bloch sphere in any direction we like. This means we are able to explore the full Hilbert space of each of our qubits.
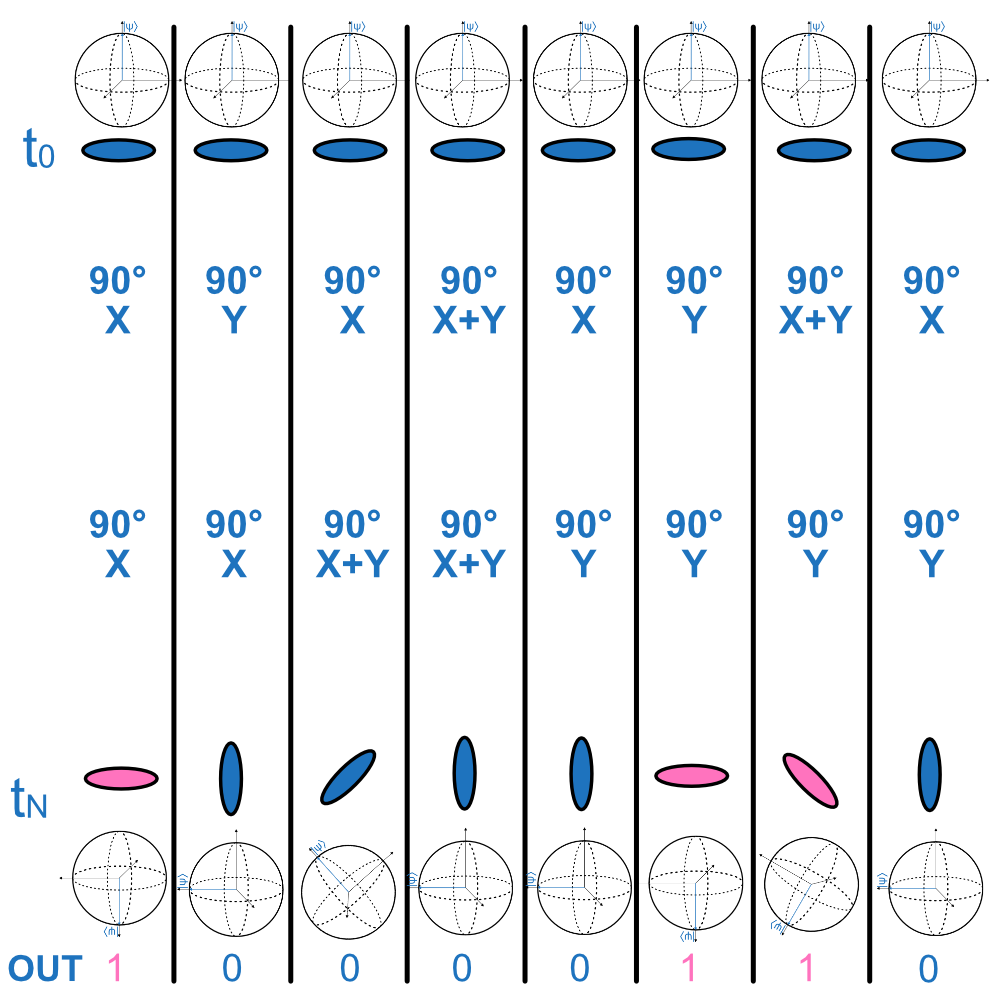
We start our quantum computer in the 00000000 state. This is labelled with 
. As we move down the diagram we show the computer at different times. We perform two gates on each qubit. These are seperate from each other and so are unaffected by the other qubits. We can consider them to be isolated and therefore model each qubit individually without considering their neighbours. When we measure the rotated qubits, their output depends probabilistically on the state on the direction of the arrow in the Bloch sphere. This is roughly equivalent to the state of a coin whose final state depends on the direction it is balanced in.
But so what? This in itself is not that useful. We can imagine replacing our qubits with actual coins. In fact, this would contain more information than real qubits, since when we measure them we destroy the information about its state!
Quantum Entanglement
Quantum entanglement is the second key ingredient in understanding what makes Google’s algorithm so complicated. Entanglement is the process of taking a set of qubits, creating a superposition of at least two configurations, and altering their collective states. This is easiest to see for two qubits. By applying an entangling operation on two neighbouring qubits, originally in the state, we arrive at the new state
![\[|\psi\rangle=\frac{1}{\sqrt 2}\left(|00\rangle+|11\rangle\right)\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-1ea7a6fb5727dfa0e58e07015f891a2b_l3.png "Rendered by QuickLaTeX.com")
To understand why its so shocking that we can prepare this state, we have to imagine what will happen when we measure each qubit separately. We first measure the first qubit. The probabilities of measuring a 0 or a 1 are both 50:50. If we measure a 0 on the first qubit, we will know instantaneously without a doubt that the second qubit is also a 
before we measure it. The same goes for if we measure a 1. We know for sure that the second qubit will be in the 1 state. This also works if we prepare an entangled state and separate them to either side of the universe. The second state will be known by the person who measures the first qubit instantly and without communication, before the second qubit is measured.
The Algorithm
The problem with qubits is that they are very unstable. Google has been working for years to keep their qubits stable for longer and longer times. Their qubits can now survive for a few seconds. This really isn’t very long. In order to demonstrate a calculation that cannot be performed by a classical computer, they needed to run a calculation which acted very fast.
The algorithm they chose alternates between single-qubit gates, in an order that is random but determined before the experiment starts, followed by entangling gates in between these operations. The entangling gates rapidly entangle a maximal number of pairs of qubits at a time, in an alternating pattern, entangling each neighbour systematically. For our 8 qubit example, we can visualise this with a special entangling gate, which I represent with tangled rainbow strings.
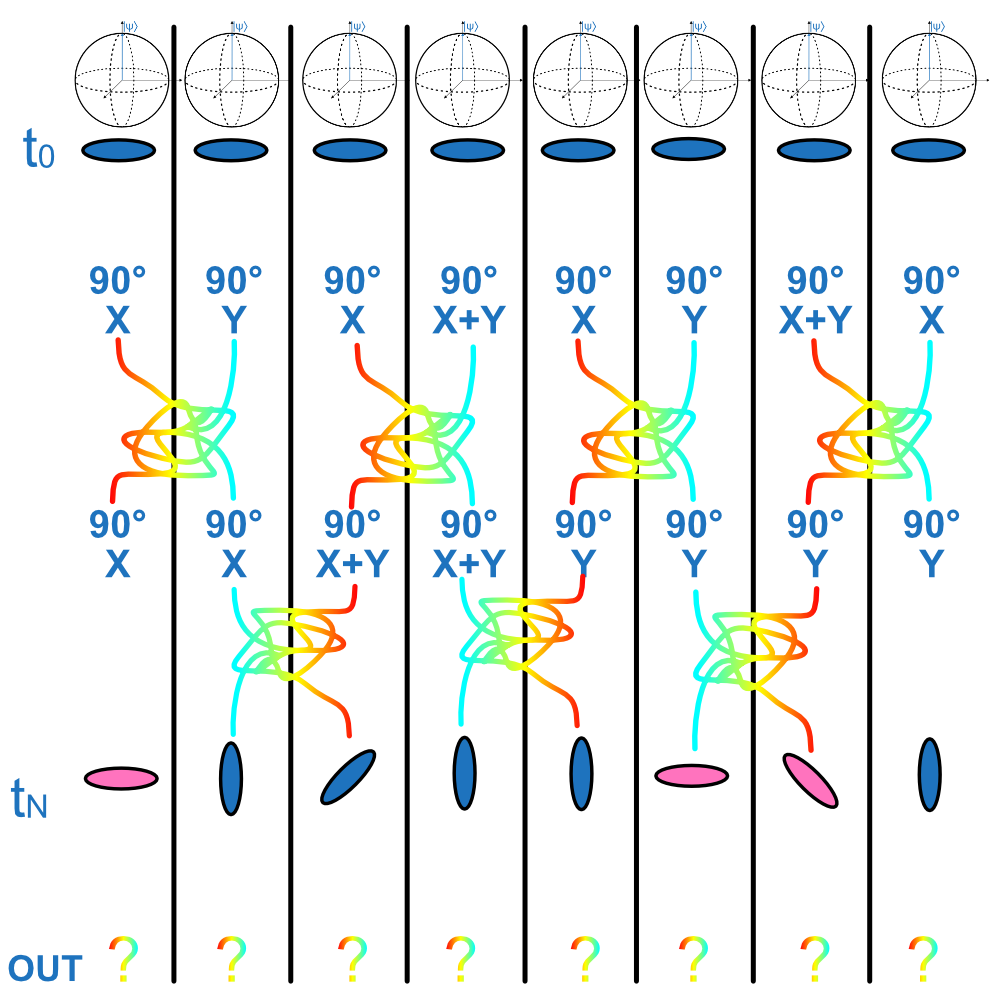
The Entangling Gate
The entangling gate that Google used is actually a combination of two separate gates: the iSWAP and a partial cPHASE gate. To understand what these do, consider the ordinary SWAP gate. This gate has the effect of switching the values of two quantum bits. We can see its effect on the basis state of the two bits.
![\[|00\rangle\to|00\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-804782930e51160f9c55730a0ec8516c_l3.png "Rendered by QuickLaTeX.com")
![\[|01\rangle\to|10\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-14a11cc2357f2444e11de2918f550a6f_l3.png "Rendered by QuickLaTeX.com")
![\[|10\rangle\to|01\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-ce0bf28ec202954931044e5d25051f67_l3.png "Rendered by QuickLaTeX.com")
![\[|11\rangle\to|11\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-805cc9b8fc072996c349504f8964fd47_l3.png "Rendered by QuickLaTeX.com")
The iSWAP is very similar, except it adds a 
phase to the state if the state is different from before the gate acts upon it:
![\[|01\rangle\to-i|10\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-55d60181a12b23a1f909a913863bbc59_l3.png "Rendered by QuickLaTeX.com")
![\[|10\rangle\to-i|01\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-be248c808e804db27df14062880b79b1_l3.png "Rendered by QuickLaTeX.com")
Finally, the cPHASE gate has the effect of rotating the phase of the state by 
if both bits are in the state:
![\[|11\rangle\to e^{2\pi i/6}|11\rangle\]](https://phys.cam/wp-content/ql-cache/quicklatex.com-5d7630f21ab601eb2f0df83dfbb50b15_l3.png "Rendered by QuickLaTeX.com")
Crucially, the combination of rotation gates and entanglement means that it no longer makes sense to write the qubits as separate entities. Their states have become entangled with each other, and detangling them without destroying their states is impossible!
Performance
The purpose of rapidly alternating between rotations and entanglement gates is to explore the Hilbert space as quickly as possible. The idea is to create the most quantum-like state before they measure the qubits and destroy their entanglement and superposition. Using the naive encoding procedure I outlined above, 53 qubits could, in theory, store around 9 petabytes of information. Of course, this is not practical for actually storing data, but by performing calculations on this amount of data we can generate a series of operations which classical computers will have a very hard time replicating. This is exactly what Google did.
They were able to show that their calculations, which took 200 seconds, would take a supercomputer 10,000 years to reproduce.
Or have they?
IBM have – with spectacularly good timing – just released a blog post and scientific paper which claim that Google may have claimed their victory a bit too early.
By making use of a clever and novel technique, they claim that it should be possible to run the same calculations in a much smaller time-frame, even on a classical computer. In fact, what Google claimed would take 10,000 years to calculate, may only take a couple of days. However, IBM’s result is only theoretical and has not yet been peer-reviewed. They have not yet done the calculation which they claim shouldn’t take long.
So what does this mean for Google’s result? Well, I still believe that Google did demonstrate a hugely important result. But the very fact that we do not live in a binary world means that the idea of defining a clear and absolute goal post is almost impossible. At the time Google’s paper was written, it was not possible to reproduce their result using any classical computer in the world. Therefore, while it may be unstable, I think it is fair to say that the epoch of quantum advantage is now.
The Future of Quantum Computing
There is still a lot of work to be done. The era of quantum advantage has only just begun. To demonstrate algorithms which are useful will take a lot more work. However, this proof of concept shows that the path looks bright and that the work should eventually pay off.
Meanwhile, over the next few years, many young scientists will consider entering the field. They will read the headlines and make decisions about their path based on the way the quantum computation community presents itself. Ultimately science should be accessible to all. I support projects and movements to eradicate discrimination and harassment within science. If using a new phrase will lead to a more welcoming atmosphere for even a fraction of the population, I believe it is the right thing to do.
As the community becomes larger and the need for quantum engineers grows, I am excited to be beginning my journey into the field during the beginning of the era of quantum advantage. The scale of the advantage may not be known until we look back on this moment in the years to come. However, the result is one of hopefully many exciting demonstrations of the extraordinary possibilities of quantum computation.
