Sufficient Condition for Universal Quantum Computation Using Bosonic Circuits
CC, Alessandro Ferraro, and Giulia Ferrini. PRX Quantum 5, 020337 (2024).
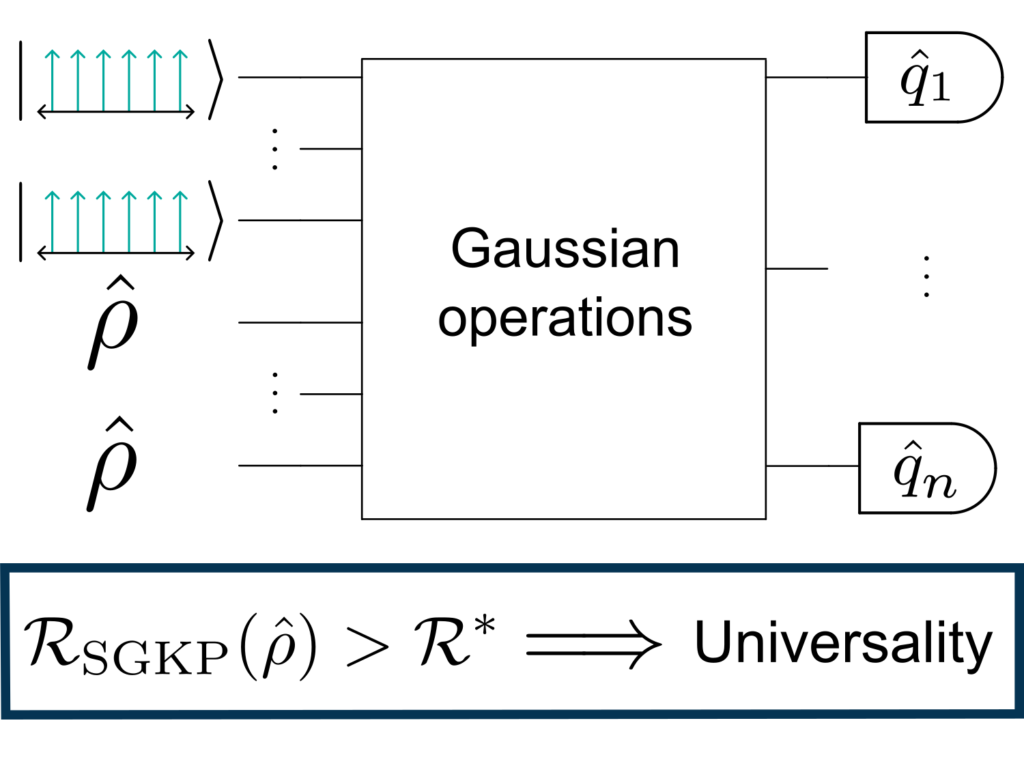
Using ideas from quantum error correction, we formulate a general framework for mapping continuous-variable states onto qubit states, proving two main results. First, we provide a resource-theory grounded interpretation of these mappings, thereby showing that they yield a rigorous way to extract qubit quantum information from a continuous-variable state. Second, we use known results in the resource theory of quantum computation for qubits to establish our sufficient criterion for continuous-variable states.
Vacuum provides quantum advantage to otherwise simulatable architectures
CC, Alessandro Ferraro, and Giulia Ferrini. Phys. Rev. A 107, 062414 (2023).

We demonstrate that a class of continuous-variable circuits are simulatable on a regular computer (these include Clifford circuits, i.e. simulatable qubit circuits, and beyond). Adding imperfections, either in the form of a vacuum state or by using realistic (imperfect) GKP states makes these circuits capable of universal quantum computation
Efficient simulation of Gottesman-Kitaev-Preskill states with Gaussian circuits
CC, Alessandro Ferraro, and Giulia Ferrini. Quantum 6, 867 (2022).
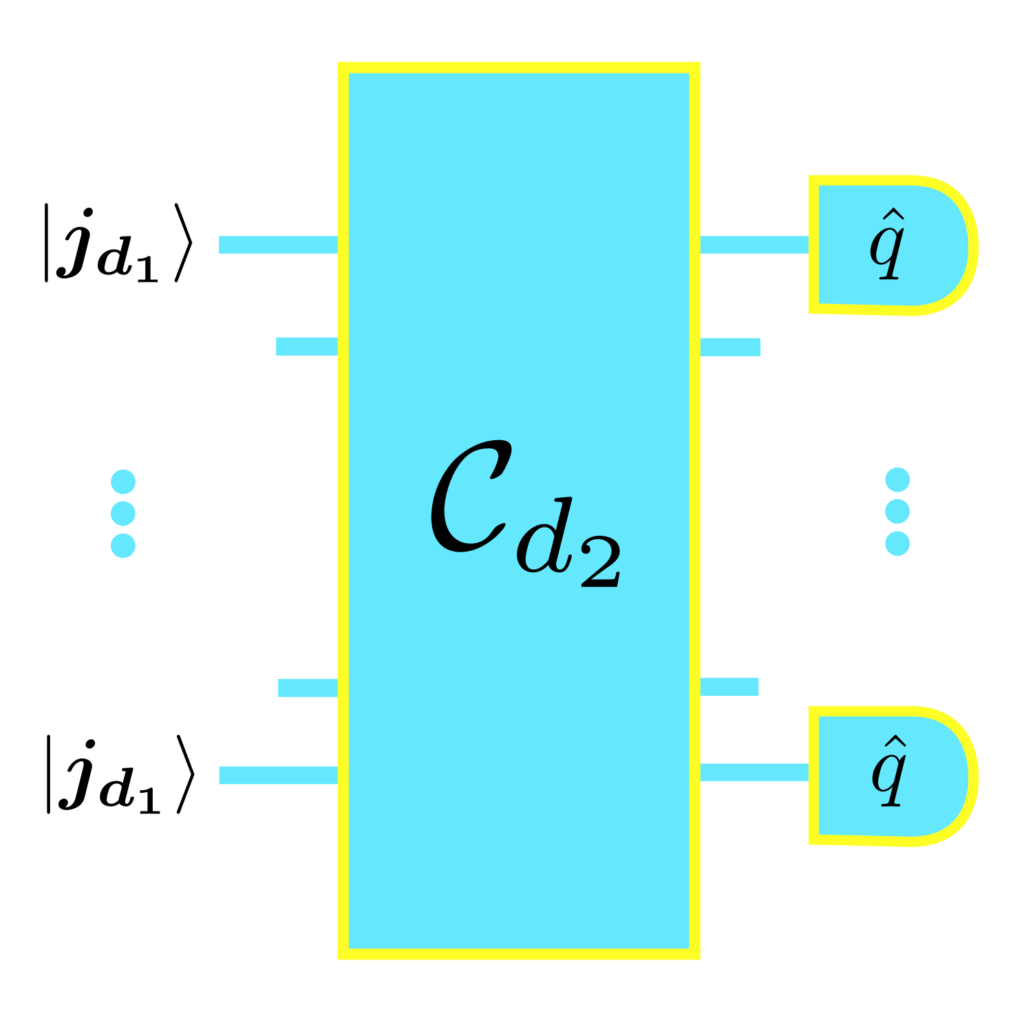
Our work demonstrates that a large class of quantum circuits with input GKP states prepared to encode computational states such as 0 and 1 is efficiently simulatable with classical computers. We, therefore, demonstrate that these circuits are not capable of achieving quantum advantage. Our findings contribute therefore to drawing a divide between computationally useful and useless architectures of quantum computers.
Efficient simulatability of continuous-variable circuits with large Wigner negativity
Laura García-Álvarez, CC, Alessandro Ferraro, and Giulia Ferrini. Phys. Rev. Research 2, 043322 (2020).
Wigner negativity is known to be a necessary resource for computational advantage in several quantum-computing architectures, including those based on continuous variables (CVs). However, it is not a sufficient resource, and it is an open question under which conditions CV circuits displaying Wigner negativity offer the potential for quantum advantage. In this work we identify vast families of circuits that display large, possibly unbounded, Wigner negativity, and yet are classically efficiently simulatable, although they are not recognized as such by previously available theorems.
